The Math of Manholes, Part One

This is a manhole.

You’ve no doubt seen them many times. But have you ever really thought about them?

Welcome to another post on the Adder! Today we delve into yet another topic that manages to squeeze math out of itself:

First, the basics. Manholes are holes in the ground. Men can go inside them, hence the name.¹https://english.stackexchange.com/questions/171125/etymology-of-manhole ²The gender issue (why manhole? why are the women being excluded?) has been discussed, but the general consensus is “the ‘man’ isn’t really like ‘man’ as in ‘male’ but rather ‘man’ as in ‘mankind’” and also “why are you asking this?”.

Where do the holes go? Sewers!³I’m not going to provide a citation for this because you can go open one and check. Also, other places, such as plumbing, gas, electricity, and the like.

Right, now we’ve got that out of the way, we can ask a question: Why are manholes round?

Actually, some of them aren’t. People in the UK and other places can see manholes in squares, rectangles, or even other shapes.

If you’re in the US or several other countries, you will see round manholes. So, why are those round?

Well, basically because they’re easier to dig, and the covers are easier to make. You will also see some websites state that manhole covers are round because they can’t fall into the hole.

See, if you have a square manhole cover, the diagonal is \sqrt{2} times the length of the side:

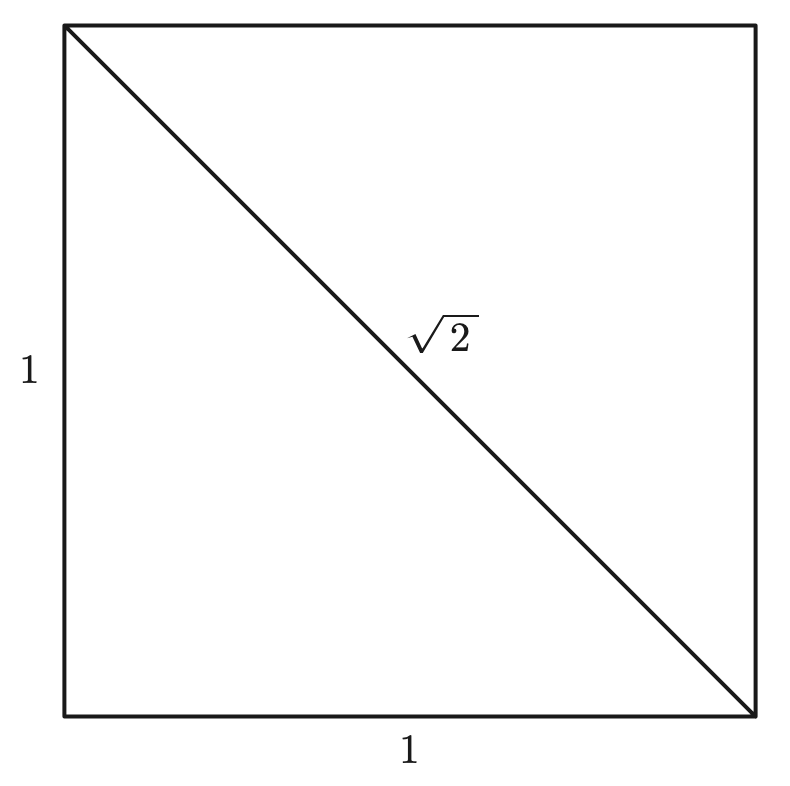
Now, watch:

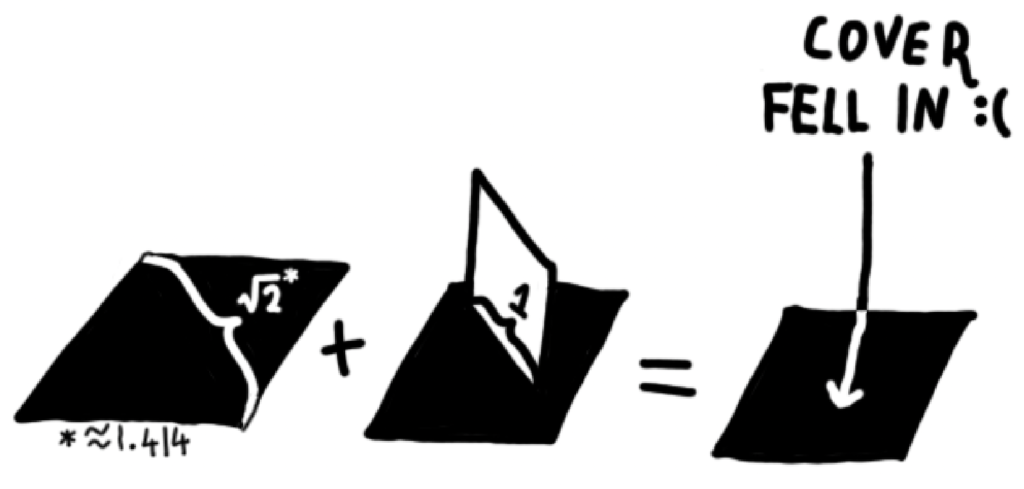
But:

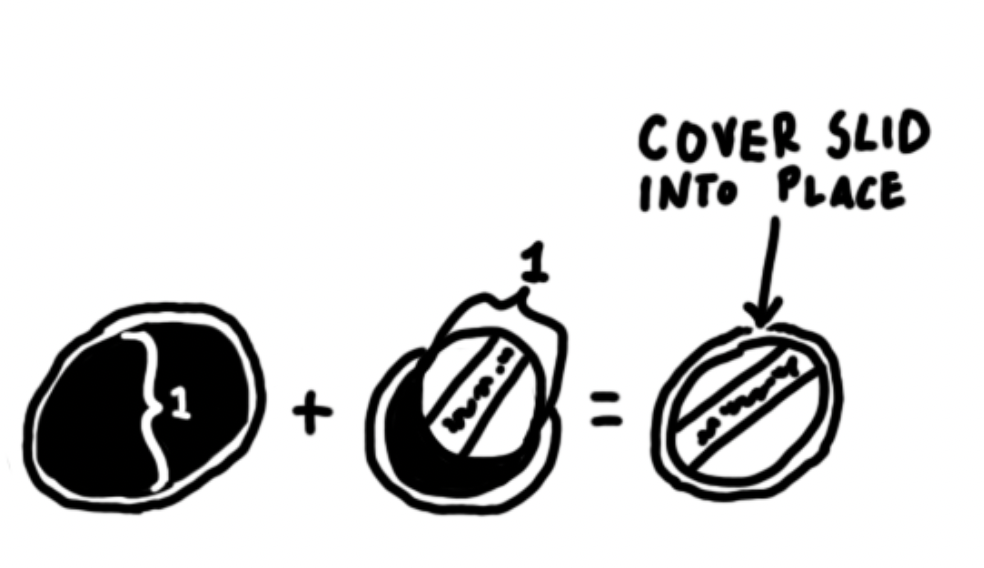
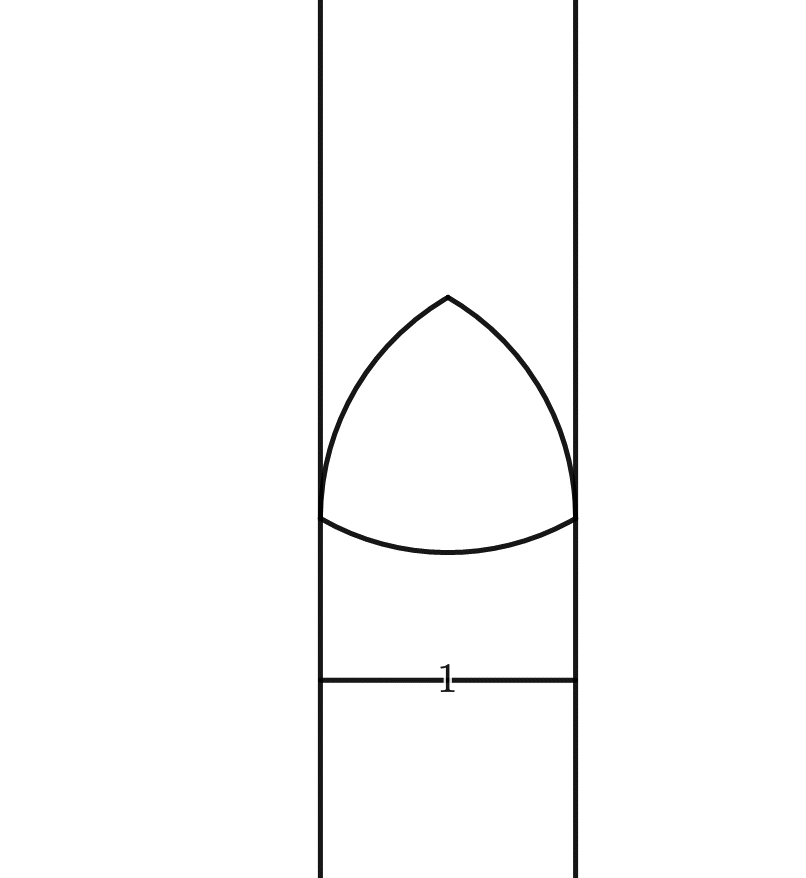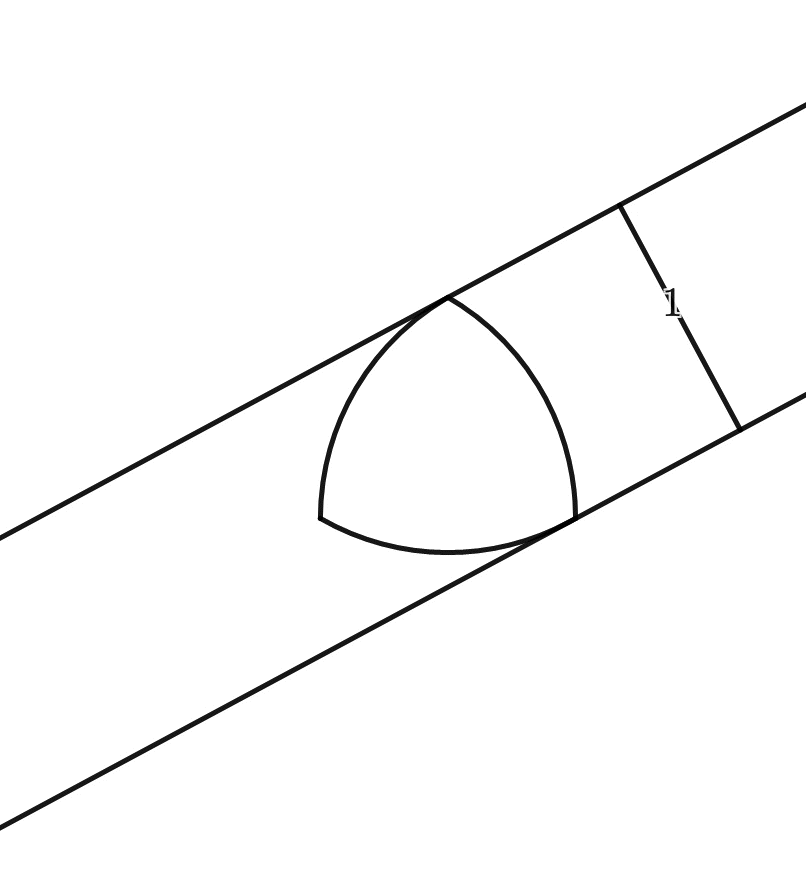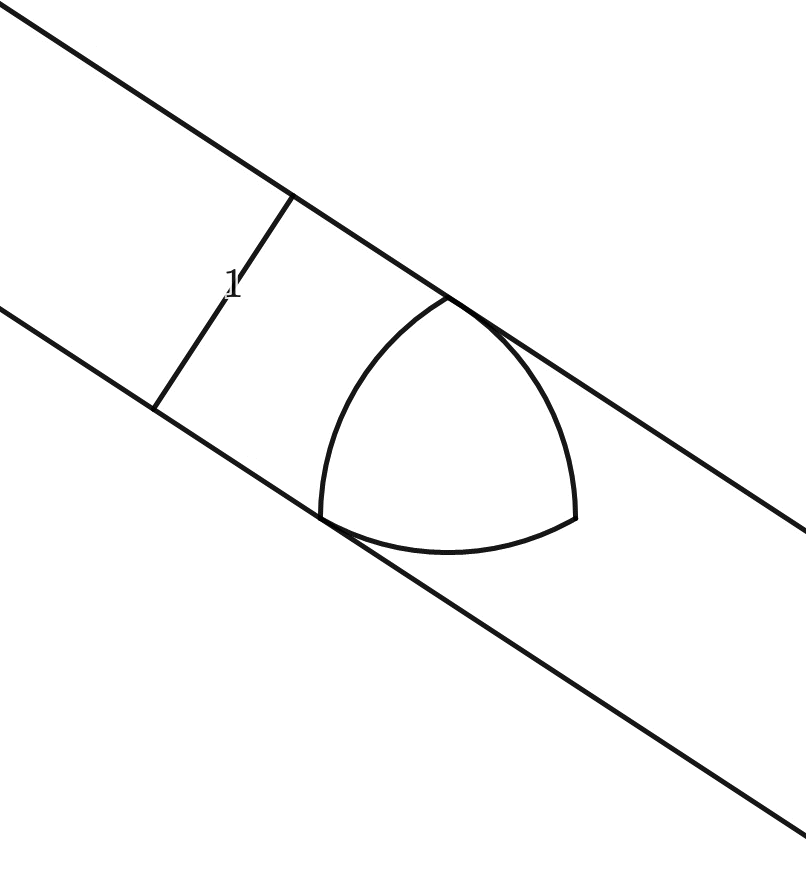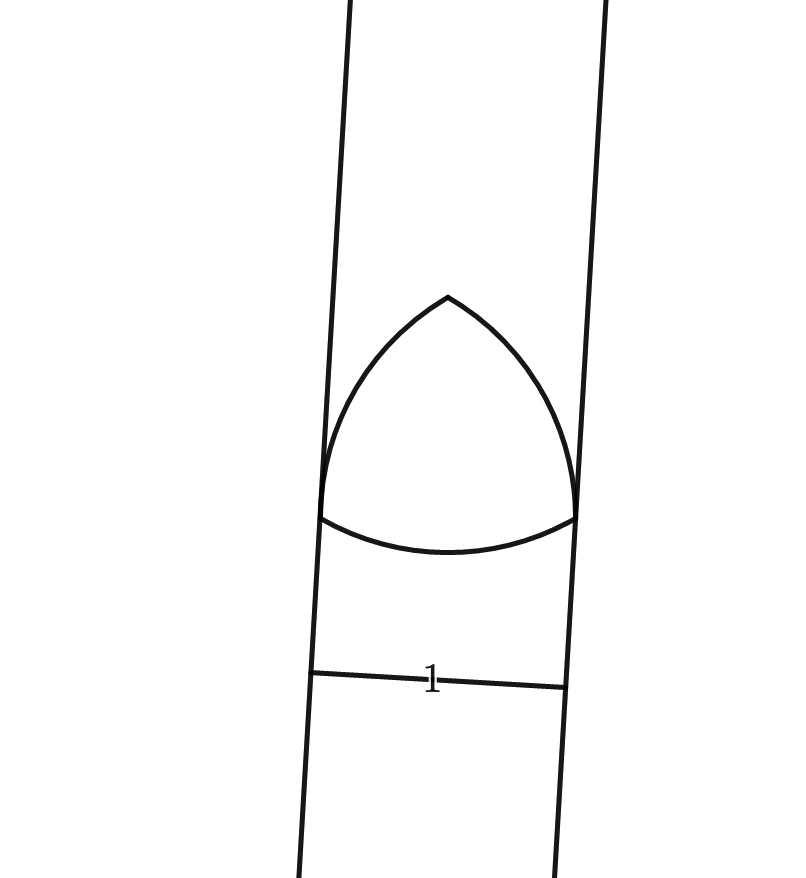
So a circle’s width is the same regardless of how it is rotated, that is, it is of constant width⁴Source code for the animations can be found here. And yes, they were a lot of fun to make.:

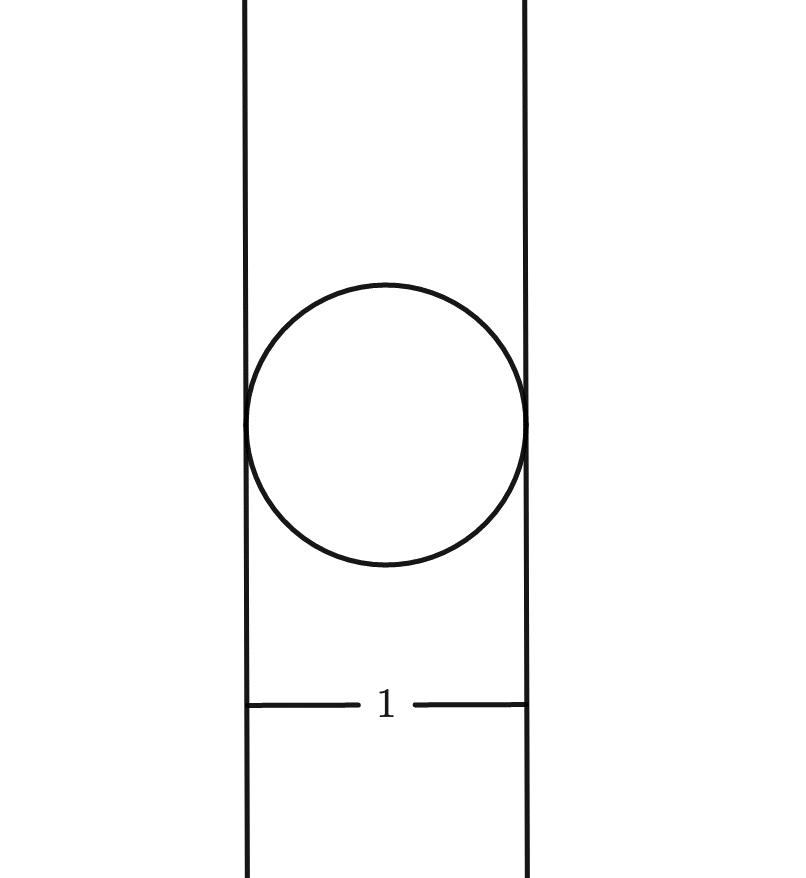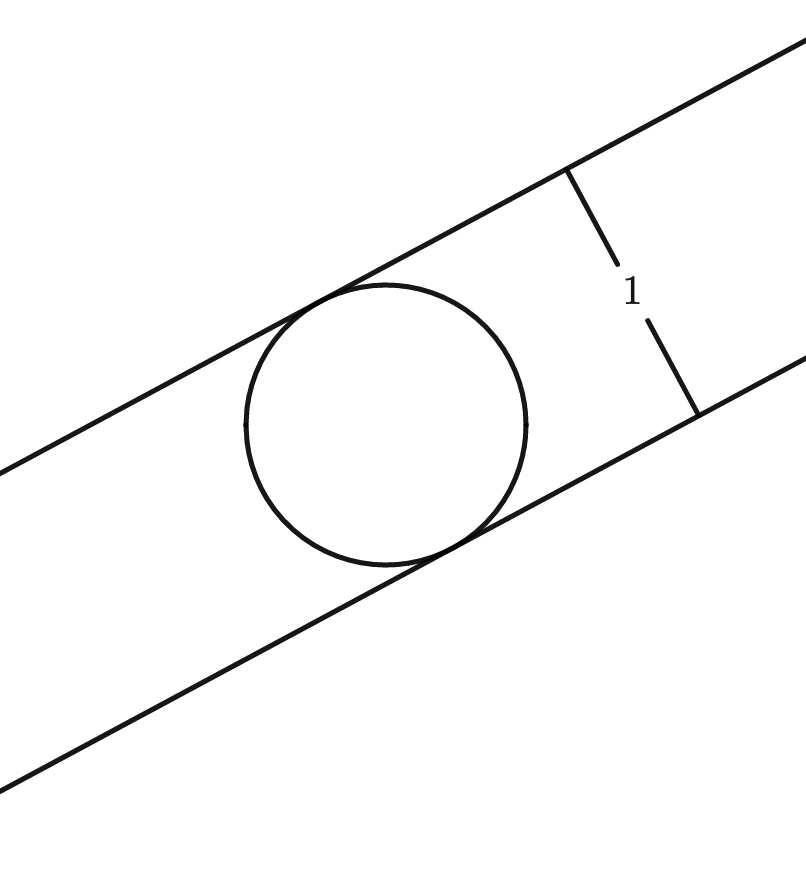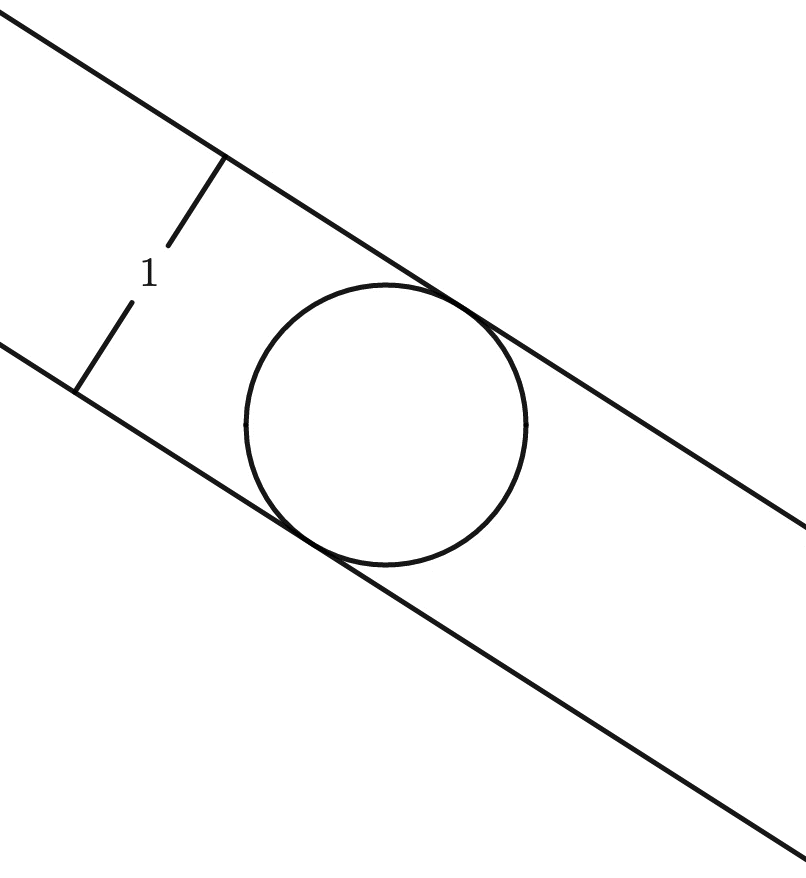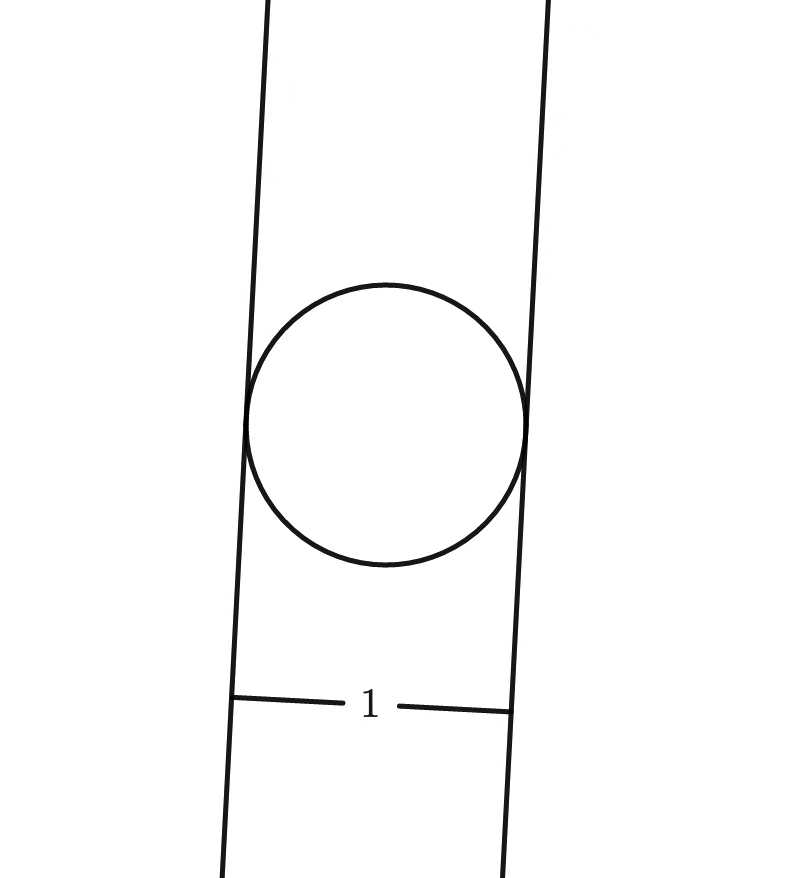
This is not so for, say, a square:

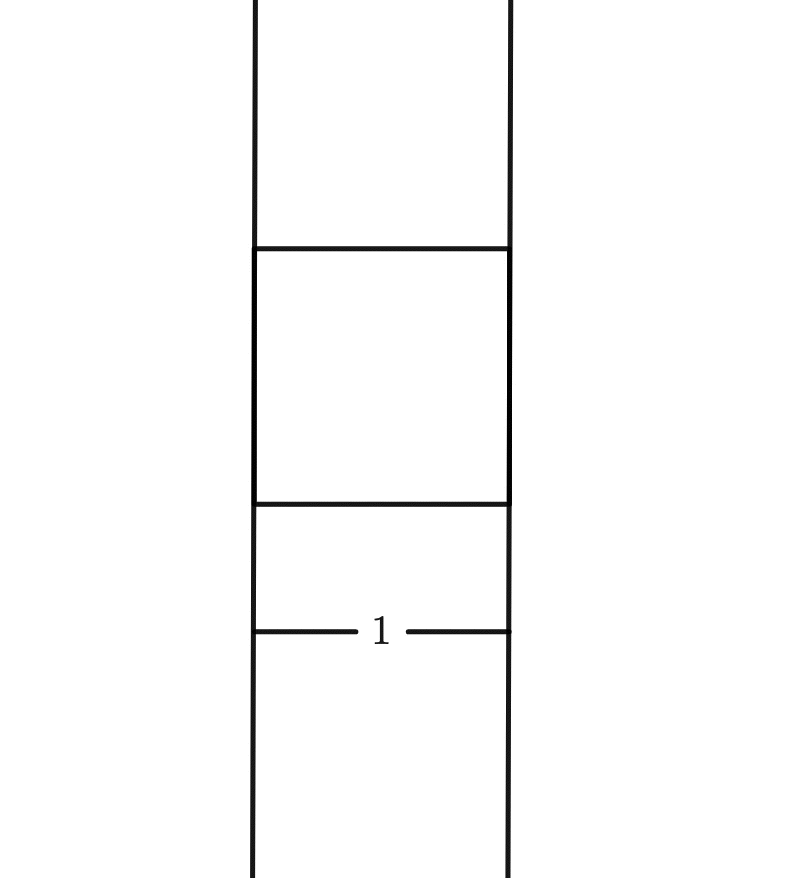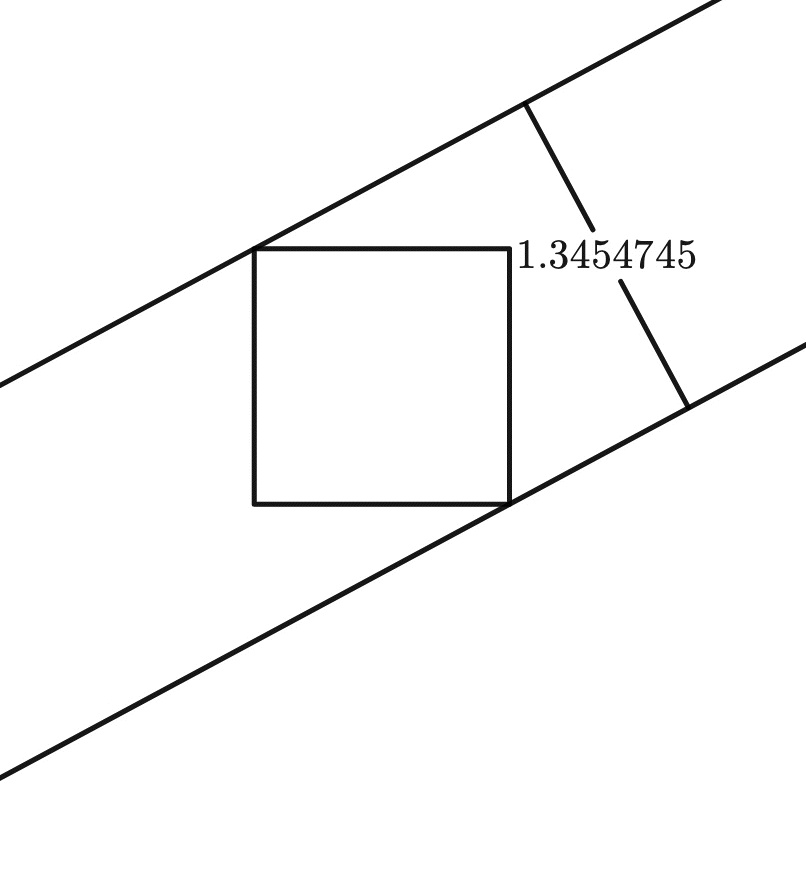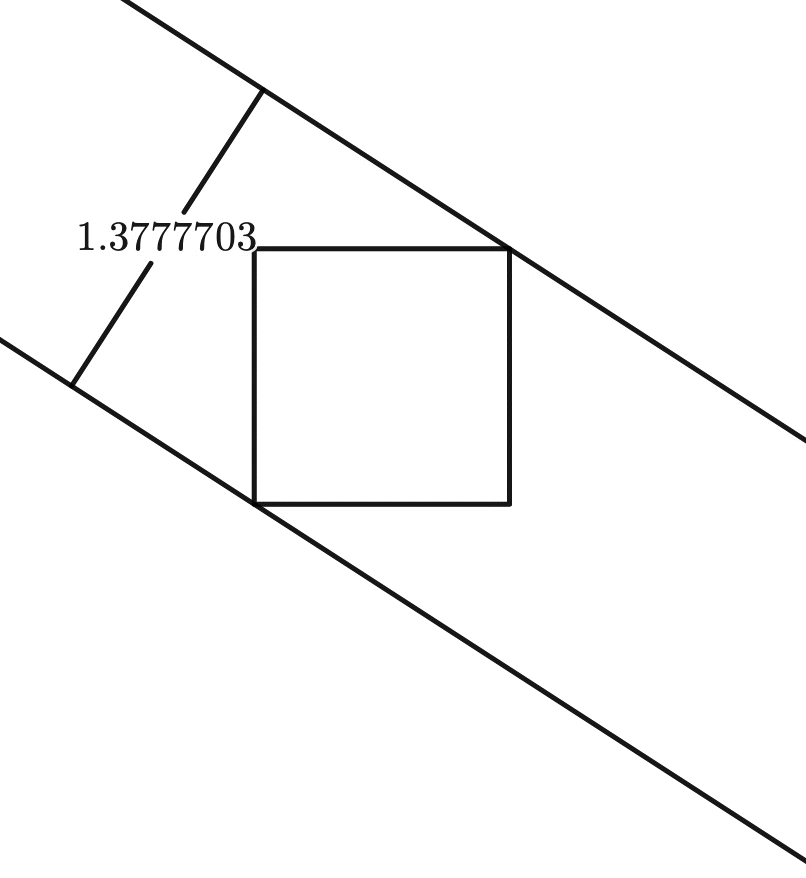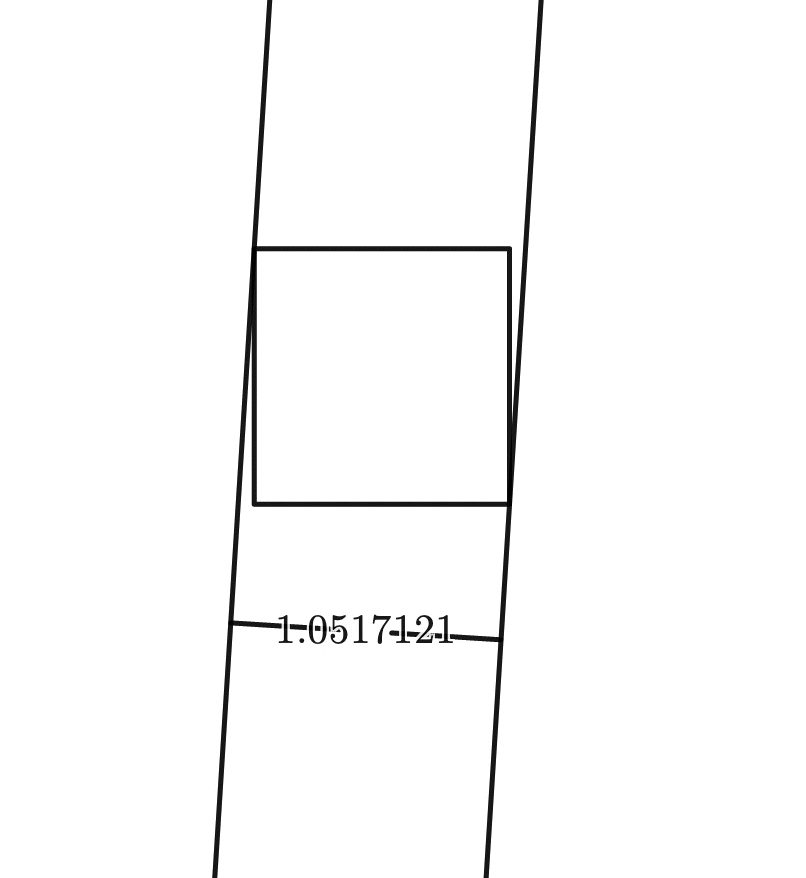
But have you ever wondered whether other shapes could be of constant width too?

Now, these are pretty hard to find by accident, so let’s try finding them on purpose. We’ll start with a triangle and see where that takes us. Obviously, the height is shorter than the side:

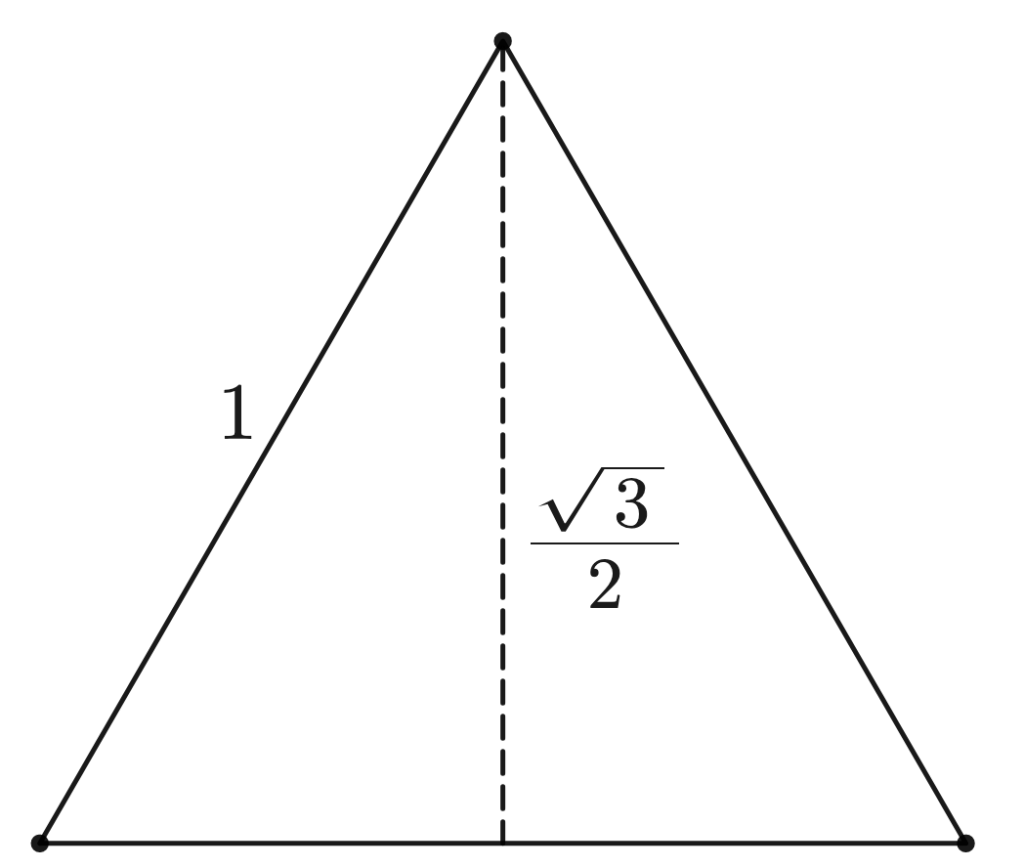
So we’ll lengthen it (the height, that is):

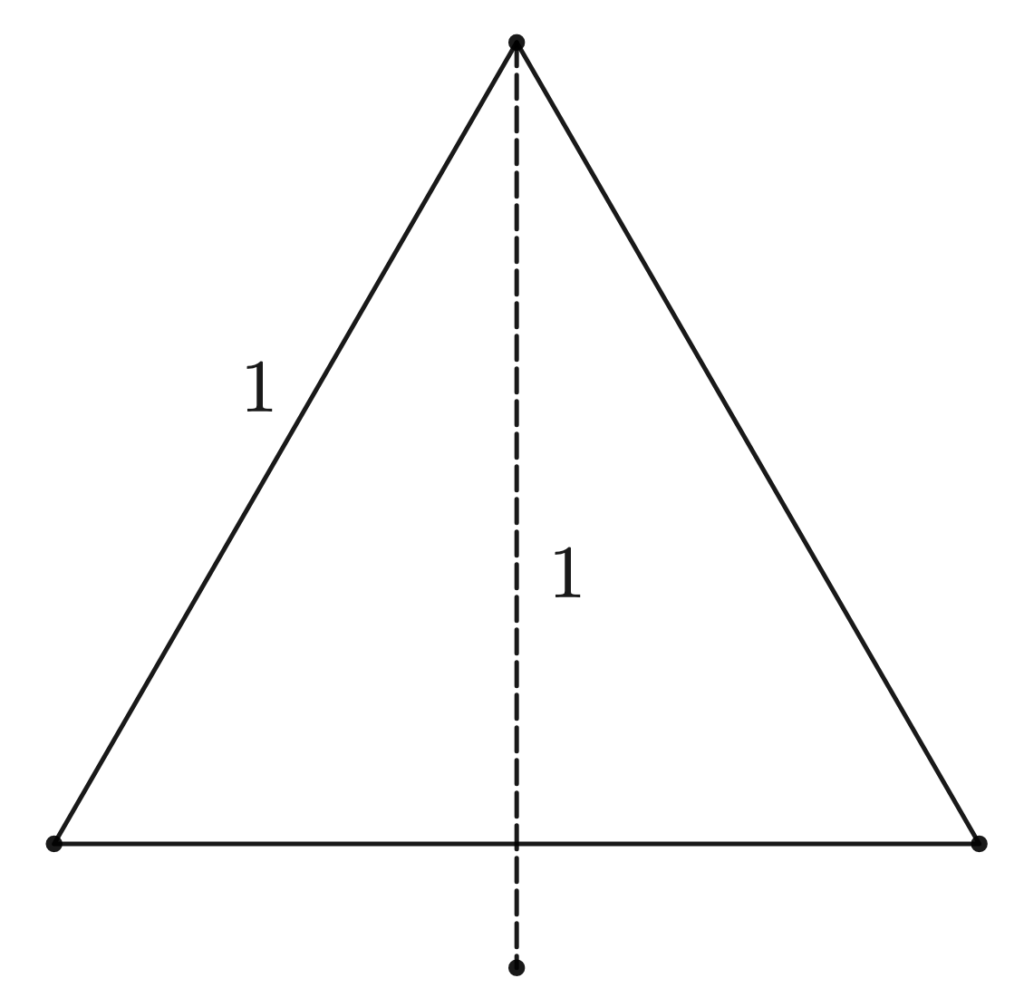
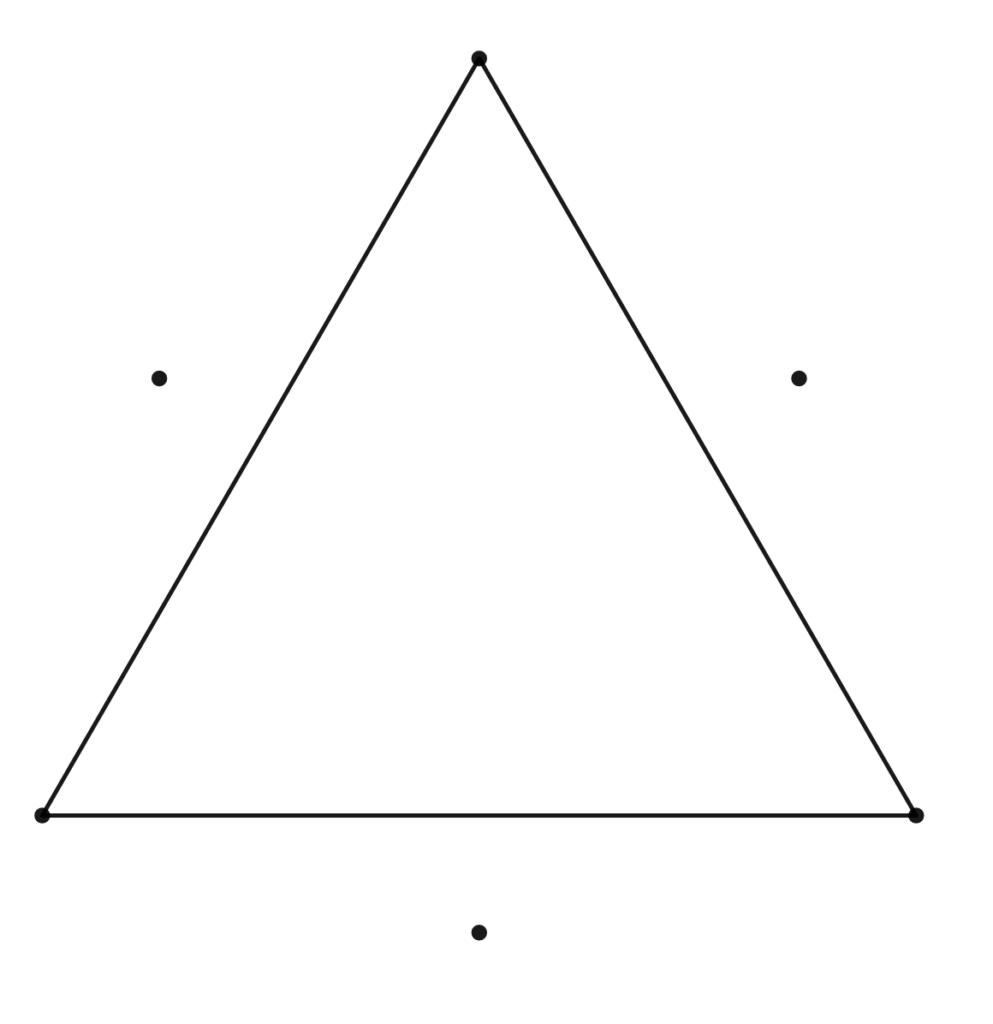
Now, we have a few extra points, so let’s connect them all together:

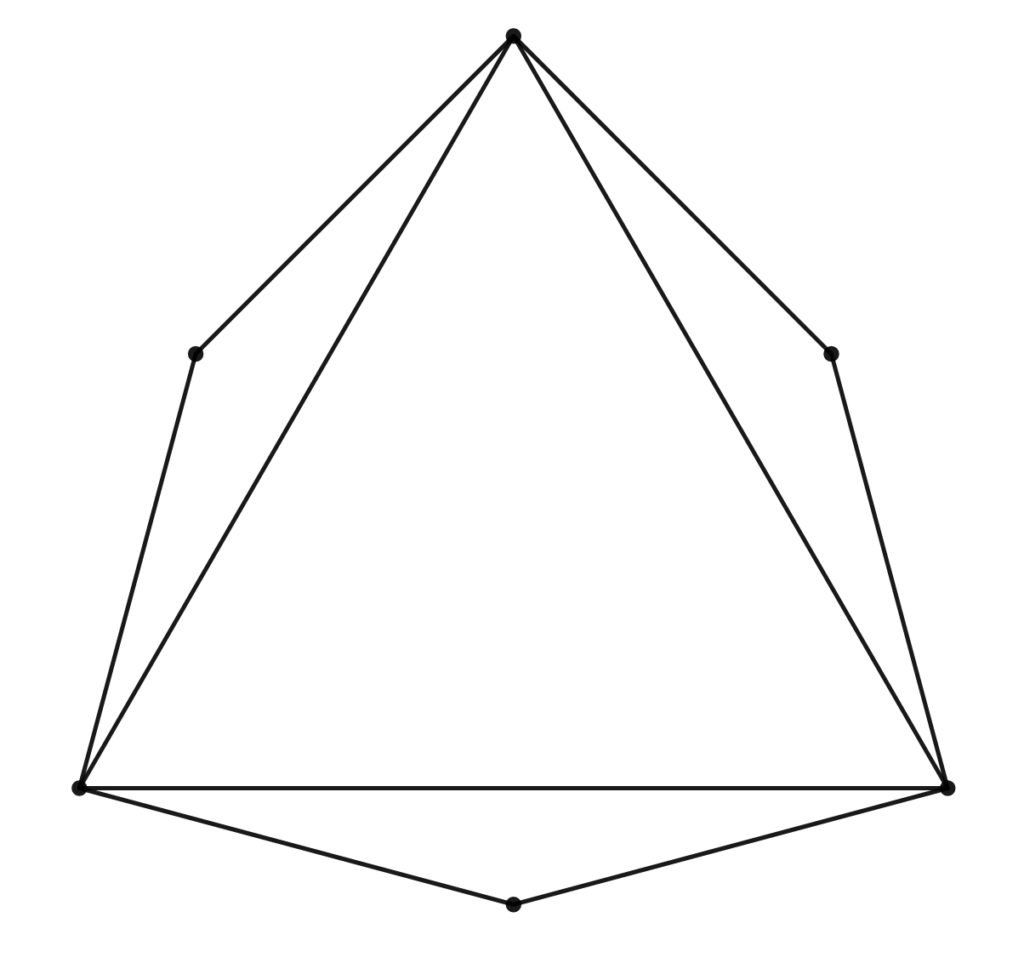
We have three lengths that are the same! This is promising. I’ll add a few more points so that you can see the pattern that’s emerging:

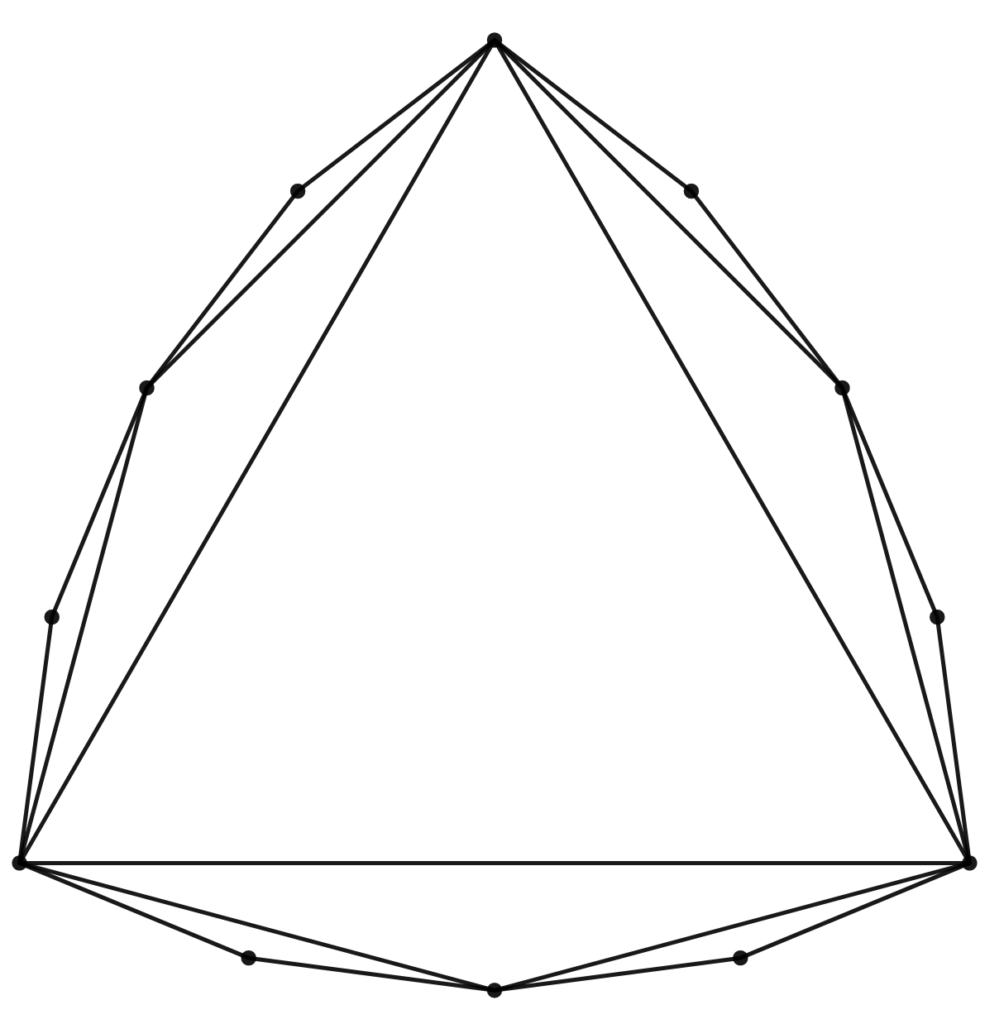
Oh, and I’ll remove the earlier triangles:

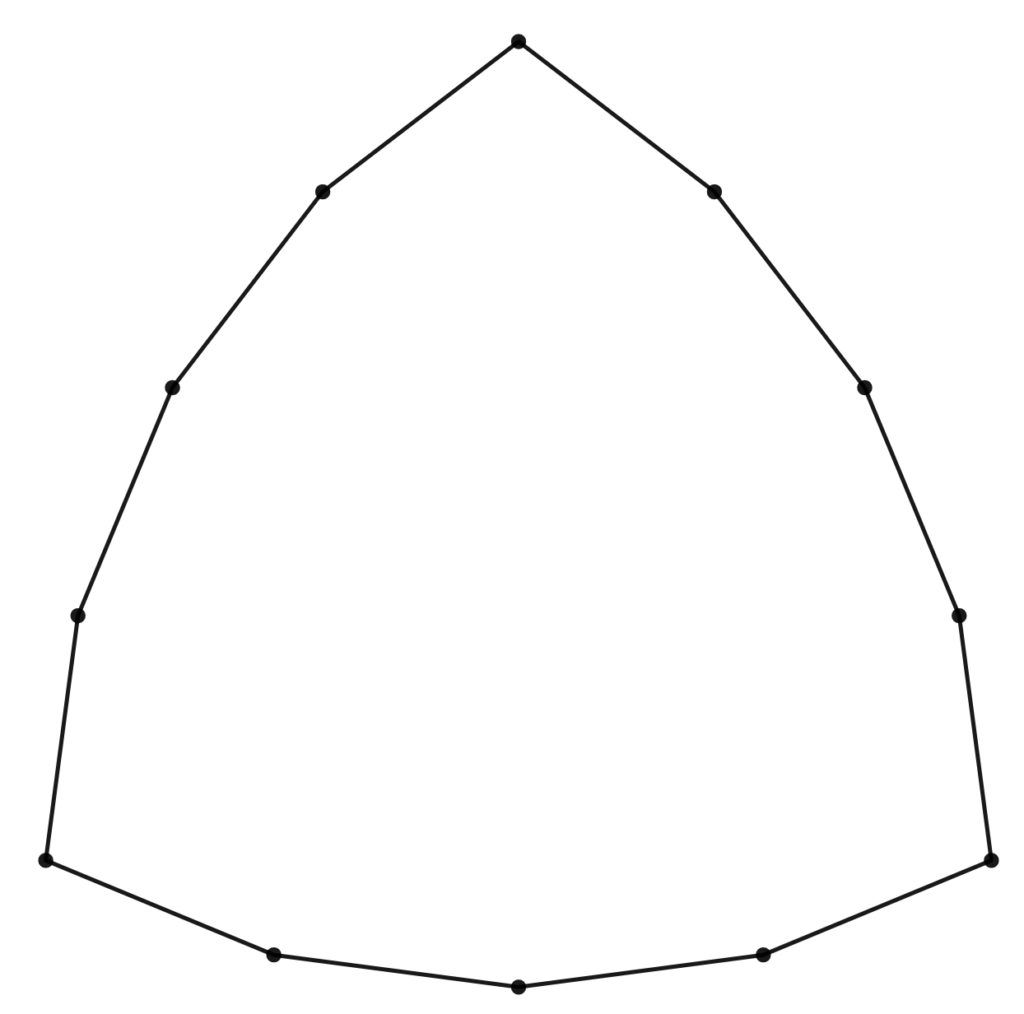
Do you see it?

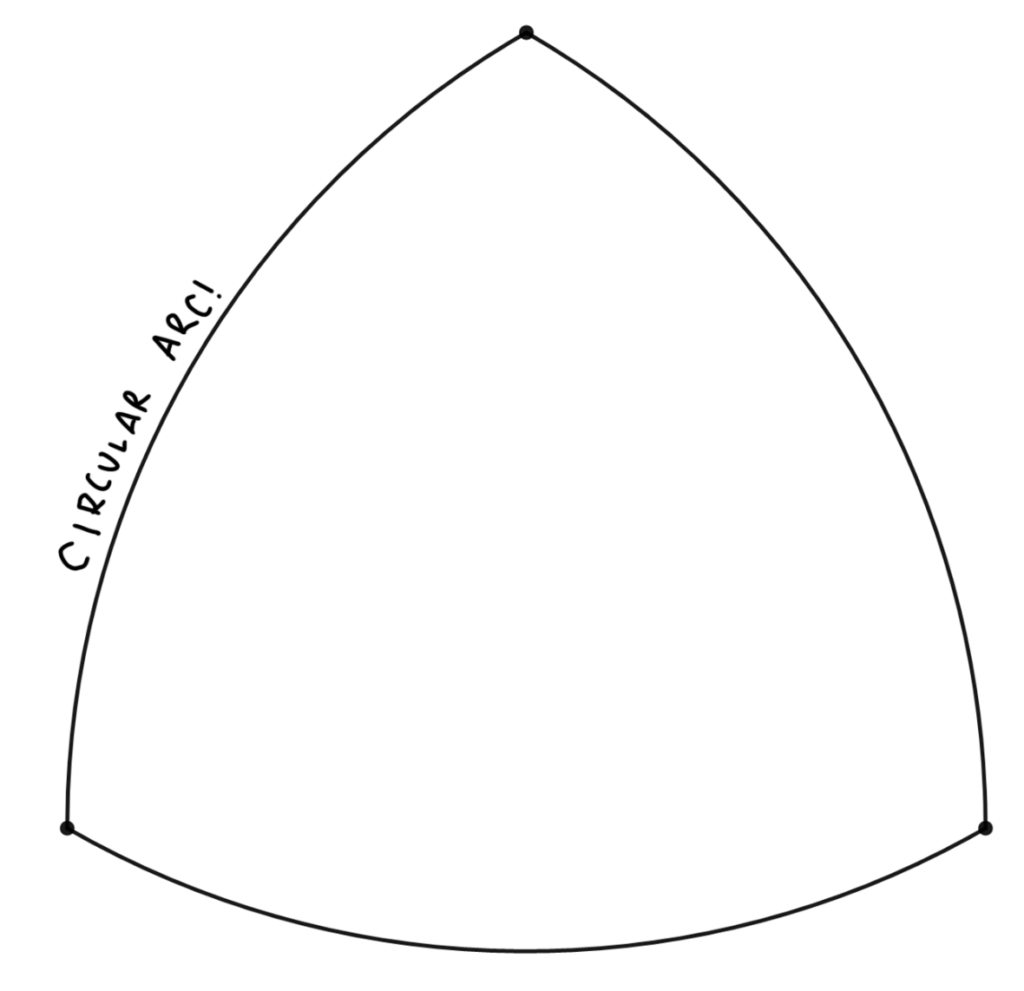
We now have what is known in the business as a “Reuleaux triangle”. This is usually described as being formed thus:

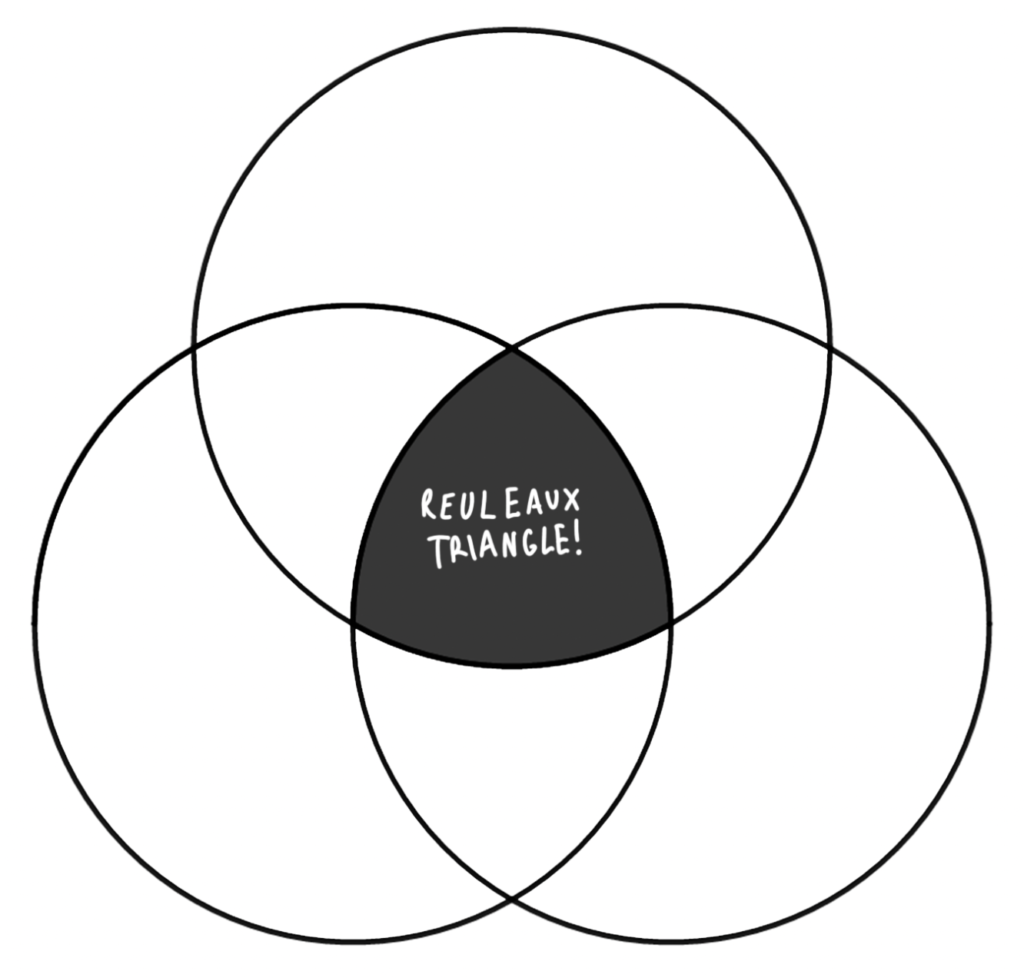
And look!

(If you look closely, this is out of sync with the circle above – the center of mass moves with the rotation. The takeaway from this is that sadly a Reuleaux triangle wouldn’t make a great wheel.)

Unfortunately, this doesn’t work if you try this with a square. If you try the intersecting circles method you get this:

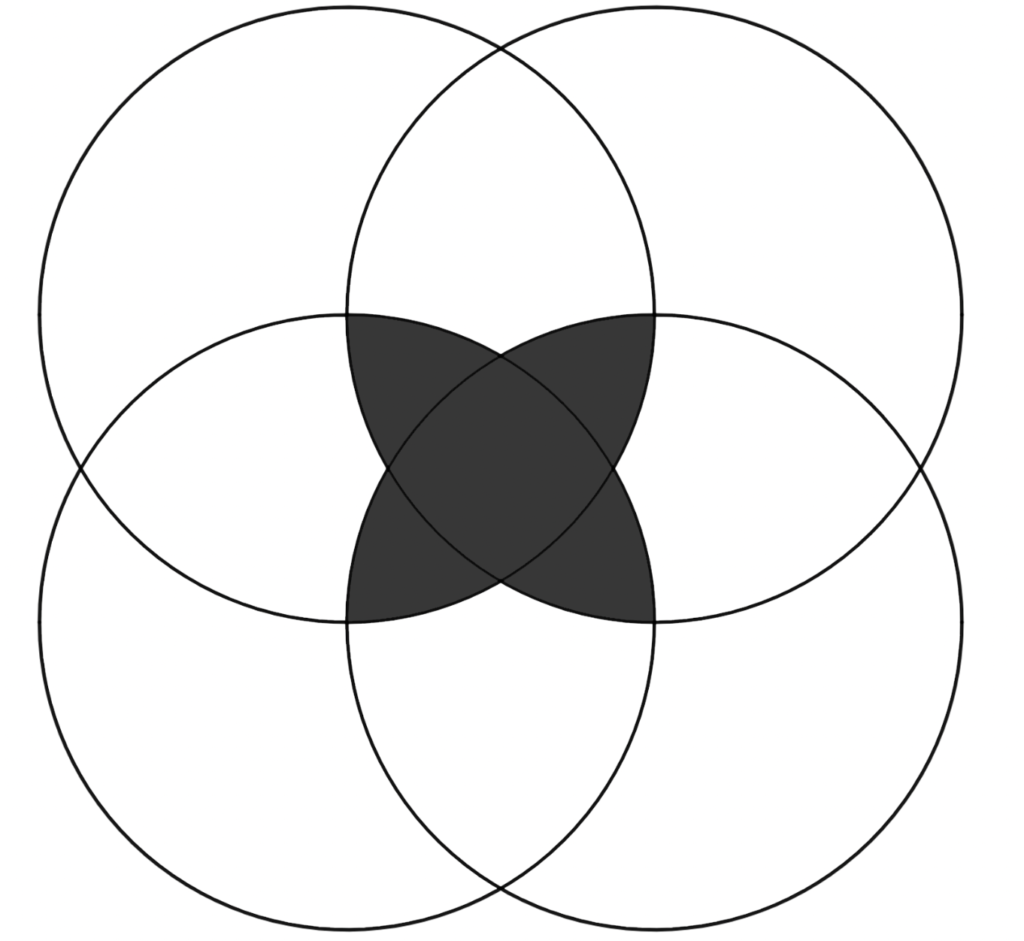
And if you try our first method, the “lengthening things until everything’s the same”, you get this:

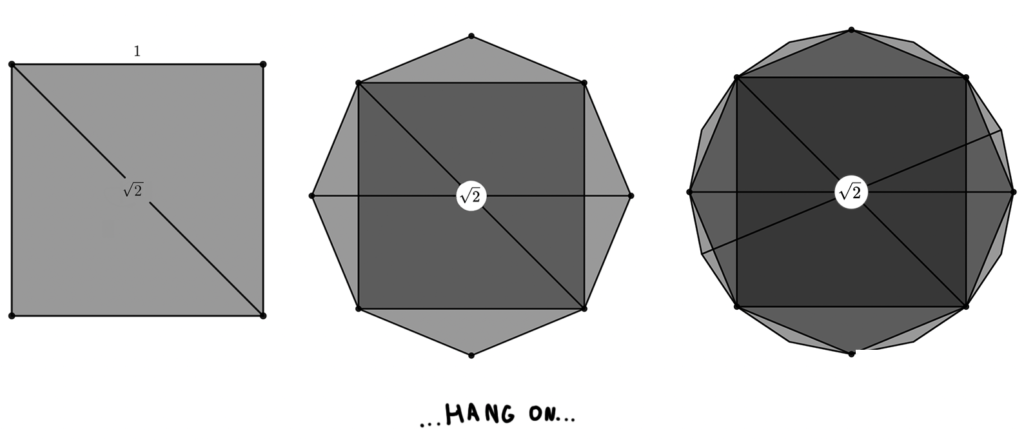
This eventually turns into a circle, which is a curve of constant width, but in a really boring kind of way:

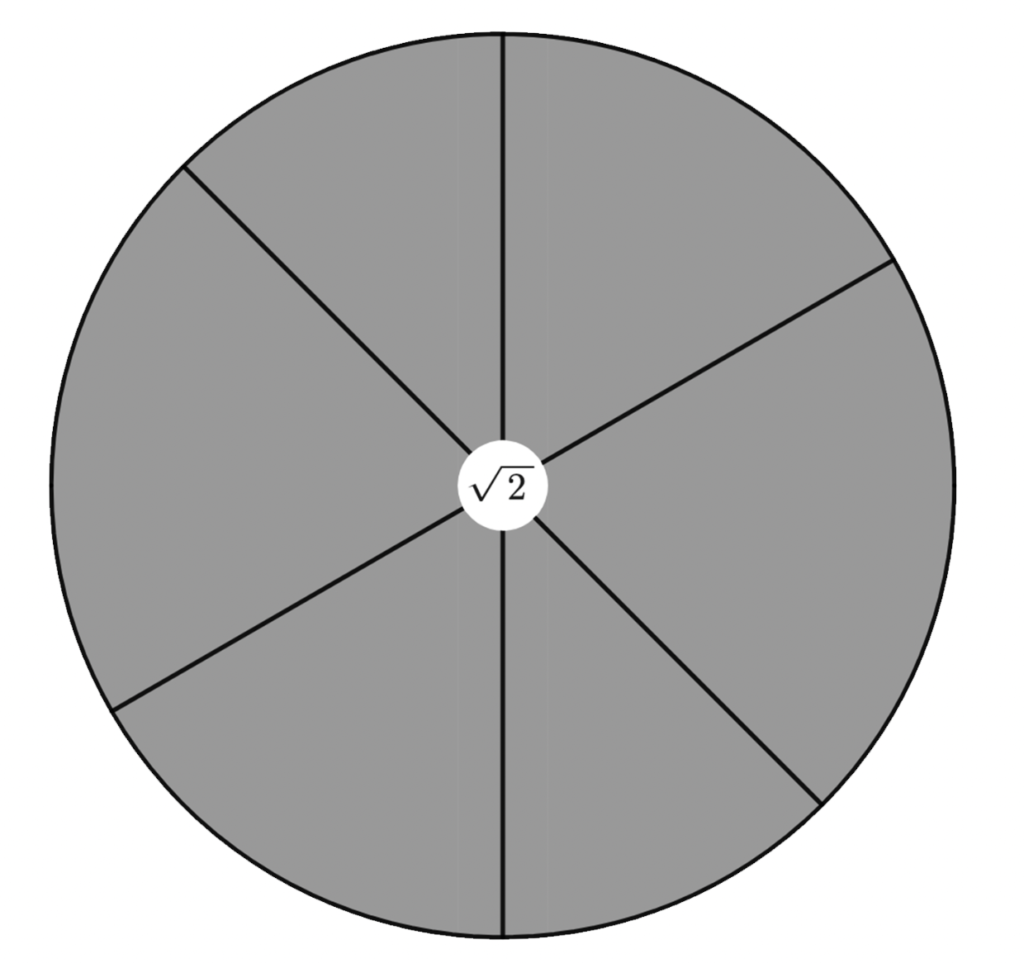
So, very sadly, we cannot turn a square into a Reuleaux square. So what’s the pattern here? Why can we turn some shapes into cool-looking curves of constant width (“Reuleaux polygons”), but we can’t for others?

For the answer, tune into part 2, coming soon! I’ll discuss the above question, as well as more Reuleaux polygons, why some manhole covers aren’t round, and more. Until then, have a wonderful day!

Sources/Footnotes

• 1
  https://english.stackexchange.com/questions/171125/etymology-of-manhole
• 2
  The gender issue (why manhole? why are the women being excluded?) has been discussed, but the general consensus is “the ‘man’ isn’t really like ‘man’ as in ‘male’ but rather ‘man’ as in ‘mankind’” and also “why are you asking this?”.
• 3
  I’m not going to provide a citation for this because you can go open one and check.
• 4
  Source code for the animations can be found here. And yes, they were a lot of fun to make.