-
Statistical Pi(e)
Statistics is probably the branch of math most closely related to science. Stats is what sets the scientific ball rolling: if you have a hypothesis, you get data, then use stats to analyze the data and come to conclusions about your hypothesis. It’s hard to imagine a way to make stats useless. Of course, this…
-
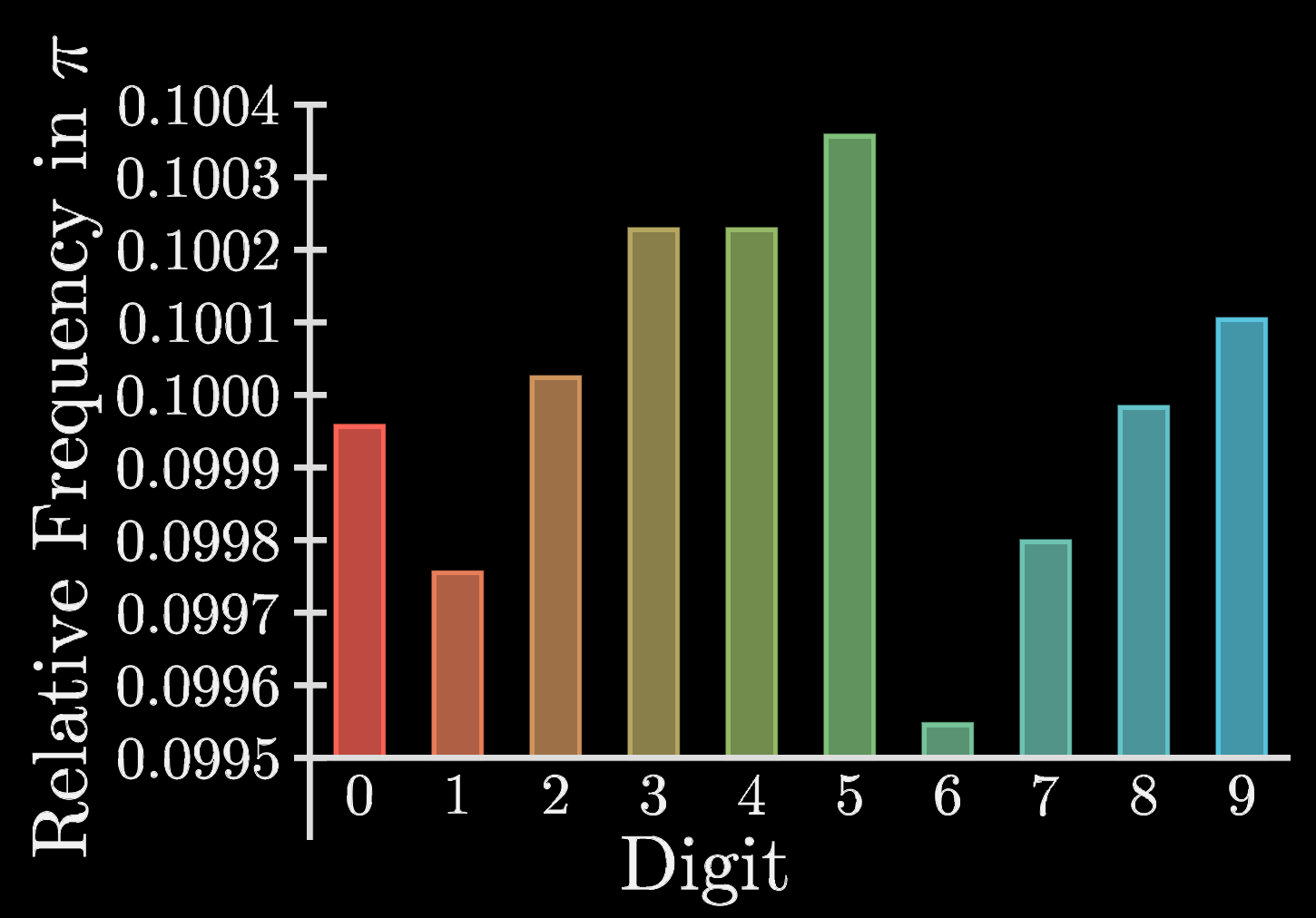
An Eccentric Approach to Conic Sections
Following are the conic sections. (They are created by slicing up two cones, hence the name.) I have taken the liberty of annotating them: Okay, so obviously they’re a lot more interesting than you may be led to believe. Hey, want to know something neat? Ellipses are very similar to hyperbolas. No, they really are.…
-
On Factorials and the Gamma Function
Factorials. The most emphatic operation. It’s notated It’s defined as: with 0! defined to be equal to 1. We’ll get to why in a moment. Now, one interesting consequence of the way the factorial is defined is that . (Why? Think about it.) What’s the point of factorials? Say you have five ambiguously-shaped objects, and…
-
That’s Life 3: The Three Types of Things
This is part 3 of a series of posts about Conway’s Game of Life; the other two can be found here and here, and here’s a supplemental post about how to play Life on a computer. I’ll start with a confession: the title of this post is sort of a lie—there are more types of…
-
Life Software
See also: Life and Life 2 I promised a post on how you can play Life (what’s Life? See the previous posts), so here it is! If you want to play Life on the web, and you don’t want to download anything, you want to use LifeViewer (https://lazyslug.com/lifeviewer/). The one quirk I’ve noticed about it…
-
That’s Life 2: The Glider
If you’ll recall, we left off from part one with John Conway sitting amazed at the “glider” that moves across the Life universe. Here it is again: Isn’t that cool? It’s cool. Want to know why? Because life is cool. Also, because Life is cool. I should note that the “R-pentomino” from the last post…
-
That’s Life
This is Conway’s Game of Life. What is this? It’s a cellular automaton: an infinite grid of squares, called “cells”, hence the name. The cells change color based on their neighbors’ colors. This is one of those math things that seem useless at first, but become intruiging, until after a decade of looking at it…
-
The Math of Manholes, Part Two
(Continued from part one) Before we start, I want to clear up a small point: Reuleaux is pronounced RUH low. Moving on. The answer to the question posed at the end of the post (“Why can we turn some shapes into Reuleaux polygons but can’t for others?”) is: if the polygon has an even number…
-
The Math of Manholes, Part One
This is a manhole. You’ve no doubt seen them many times. But have you ever really thought about them? Welcome to another post on the Adder! Today we delve into yet another topic that manages to squeeze math out of itself: First, the basics. Manholes are holes in the ground. Men can go inside them,…
