That’s Life 3: The Three Types of Things

This is part 3 of a series of posts about Conway’s Game of Life; the other two can be found here and here, and here’s a supplemental post about how to play Life on a computer.

I’ll start with a confession: the title of this post is sort of a lie—there are more types of patterns than just three, but there are three major types, and those are still lives, oscillators, and spaceships.

Still lives are those patterns which, once put on the grid, do not change. Ever. They just sit there, looking like the inanimate patterns they are. You’ve already seen the block and the beehive, but there are other ones, and they can be called weird things. Weird names are a recurring theme throughout Life. For example, this one’s called Cthulhu: you know, that one octopus-head guy from H. P. Lovecraft?

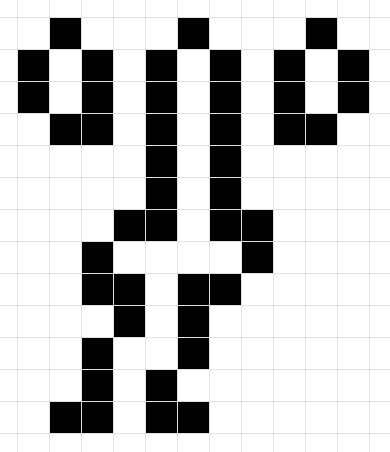
That one’s pretty uncommon to find out “naturally”, meaning that if you scribble on the Life board (random patterns are called “soups”) and evolve that, you’re not going to see Cthulhu anytime soon. Here are a bunch of still lives that are common:

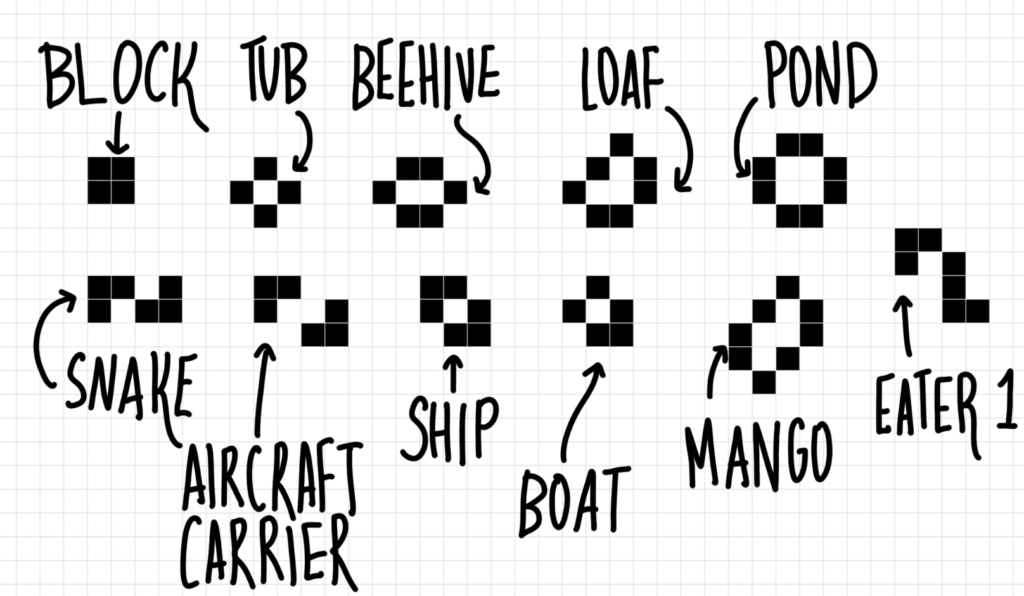
Eater 1 here deserves some merit and will be gone into a bit later in this post, when we get to spaceships.

Oscillators are patterns which do change over time, but they keep returning to the same state after a set number of generations, which we call the “period”. You’ve seen the blinker; here are a few more oscillators.

The pulsar is surprisingly common for a pattern its size; this is quickly explained by this predecessor:

It’s largely from these “pre-pulsars” that pulsars form.

And finally, there are spaceships. These translate themselves across the grid. You’ve seen the glider several times before. Here are three other spaceships which were found in the original “Mathematical Games” column by Martin Gardner:

And here are a few others (the copperhead and loafer, respectively):

There’s also the somewhat-big Sir Robin, which is unique in that it travels at a slope of 2, similar to the way a knight moves in chess. (This is also why it’s named after a knight¹Specifically, Sir Robin from Monty Python and the Holy Grail..) Here it is:

There are also other, absolutely gigantic ones, which are “constructed”, or made from smaller components interacting with each other. They’re so big (“Caterpillar” has 11.88 million cells) that my computer refuses to render them.

A few terms: the speed of a spaceship is measured in terms of the “speed of light”, or c, which is one unit per generation. No spaceship can travel at this speed; in fact, the maximum speed of a spaceship traveling orthogonally (in a horizontal or vertical line) is c/2.

Theorem 1. A spaceship traveling diagonally cannot exceed the speed of c/4.²Note that this proof only applies to spaceships travelling strictly diagonally, that is, at the compass points NW, NE, SW, and SE. Spaceships travelling at other slopes, such as Sir Robin above, are very rare, and depending on slope have different speed limits. Sir Robin is the fastest (c/6) for its slope.

In the context of the diagram below, Theorem 1 states that if the spaceship is within the light blue cells, it will be entirely contained within the light and dark blue cells until the fourth generation.

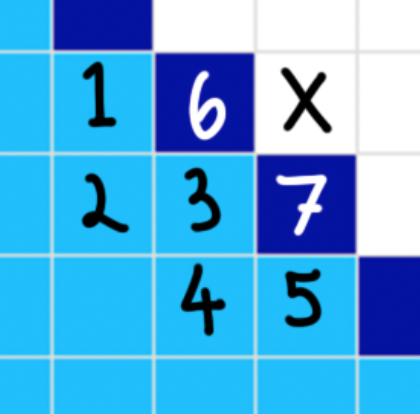
We can prove our assertion by first proving that the spaceship must be on or below the dark blue line at generation 2; that is, the cell marked X cannot be alive. If this is true, we can apply the same argument again to prove the speed limit.

Note that we are not assuming anything about the shape of the spaceship, only that it can fit inside the light blue region. This applies to all finitely large patterns, and some of the infinitely large ones too.

Anyway, onwards with the proof.

Proof. Assume for the sake of contradiction that cell X is alive in generation 2. This requires that the cells 3, 6, and 7 must be alive in generation 1. (This is because cell birth requires three live cells next to it, and these are the only cells that can be alive.) It quickly follows that in generation 0, that is, the beginning, cells 1, 2, 3, 4, and 5 must be alive. But!

If all of these cells are alive in generation 0, cell 3 would die by overcrowding; it would have four neighbors! This means that it cannot be alive in generation 1, and since cell X would not have three live neighbors, it will not be alive in generation 2. This completes our contradiction.

Now we’ve done that, we can move on to our orthogonal spaceship proof.

Theorem 2. A spaceship travelling orthogonally to the Life grid cannot exceed a speed of c/2.

This actually follows rather directly from Theorem 1. If we consider the following diagram…

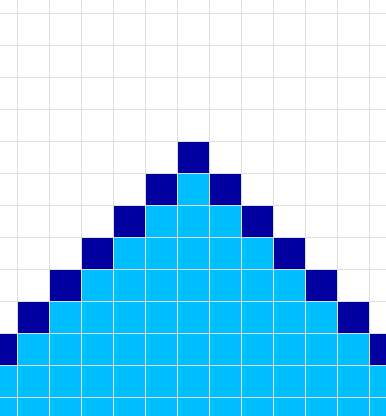
…and assume that the spaceship is contained within the light blue cells, we have already showed that it must be within the dark blue cells by generation 2. We have no need for a Q.E.D.

A bit more about spaceships before I sign off: the period of a spaceship is essentially the same thing as that for oscillators (number of generations before it repeats, or looks the same as generation 0). And eaters are patterns that “eat” spaceships. Eater 1 (remember eater 1?) is an example of one:

Eater 1 can eat a lot of things, including beehives³Okay, technically pre-beehives, which are two-by-three blocks of cells which become beehives in one generation, but eater 1 still works as a beehive eater for most purposes, since almost all beehives are formed via pre-beehives anyway., so here’s a queen bee shuttle stabilized by two eater 1s instead of blocks (this configuration has been unfathomably named “buckaroo”):

I think more is warranted on eaters, so see you in part 4!

Sources/Footnotes

• 1
  Specifically, Sir Robin from Monty Python and the Holy Grail.
• 2
  Note that this proof only applies to spaceships travelling strictly diagonally, that is, at the compass points NW, NE, SW, and SE. Spaceships travelling at other slopes, such as Sir Robin above, are very rare, and depending on slope have different speed limits. Sir Robin is the fastest (c/6) for its slope.
• 3
  Okay, technically pre-beehives, which are two-by-three blocks of cells which become beehives in one generation, but eater 1 still works as a beehive eater for most purposes, since almost all beehives are formed via pre-beehives anyway.