This is Conway’s Game of Life.
What is this? It’s a cellular automaton: an infinite grid of squares, called “cells”, hence the name. The cells change color based on their neighbors’ colors. This is one of those math things that seem useless at first, but become intruiging, until after a decade of looking at it you realize that it’s capable of simulating computer programs.
Aaaaaaand that’s the meaning of Life! Bet you didn’t think you’d find that while reading a math blog! Just goes to show how useful math can be.

Let’s go back in time. Specifically, to the 1940s.
John von Neumann is researching replication. He had a very cool idea for how a machine could replicate, but as this isn’t really relevant for what this is about, I’ll go into it in a later post. For now, I’ll just say that his idea was very similar to how it was later discovered (by Watson and Crick) that cells actually do replicate.
Von Neumann built a model of his cool idea in a cellular automaton. The model looked like this:

Unfortunately, it’s really complex and not worth going over here—if you want to find out more, here is a great place to start.
Forward in time: the Sixties.

John Conway is sitting in a faculty lounge at Cambridge University. Accounts vary as to what he is doing. Some say he’s trying to simplify von Neumann’s model1Citation: Wikipedia; others say he’s merely messing around2Citation: The Grapes of Math by Alex Bellos. Anyway, they all agree that he comes up with another cellular automaton. This one has only two states: off and on, or alive and dead.
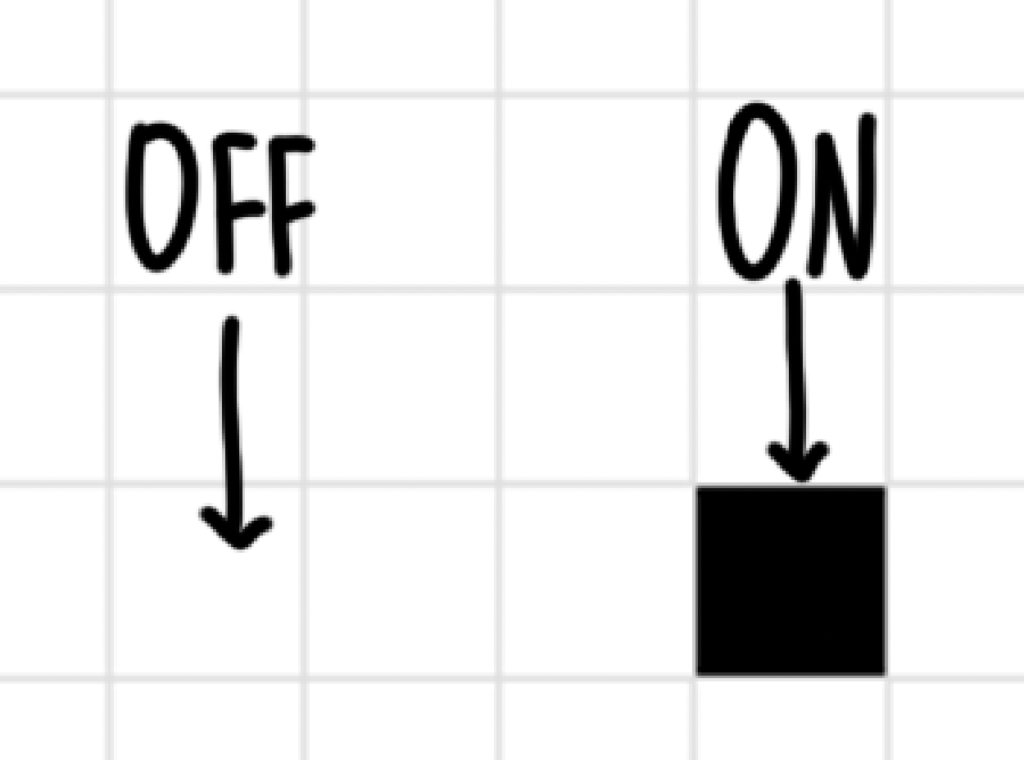
There are a few rules: if a dead cell has exactly three live neighbors (diagonals count), it comes to life, or is “born”. If a live cell has either two or three live neighbors, it stays alive; otherwise, it dies. This all happens in one unit of time, or tick, or generation, or move — usually generation, but naming isn’t too consistent.

We’ll look at a few examples to solidify this. This one’s called a block in the lingo:

And this is a “blinker”:

Conway found very quickly that this rule creates weird stuff from very simple initial patterns. Look at the so-called “R-pentomino”:

After 69 generations, it still hadn’t settled. However, an interesting pattern emerged:
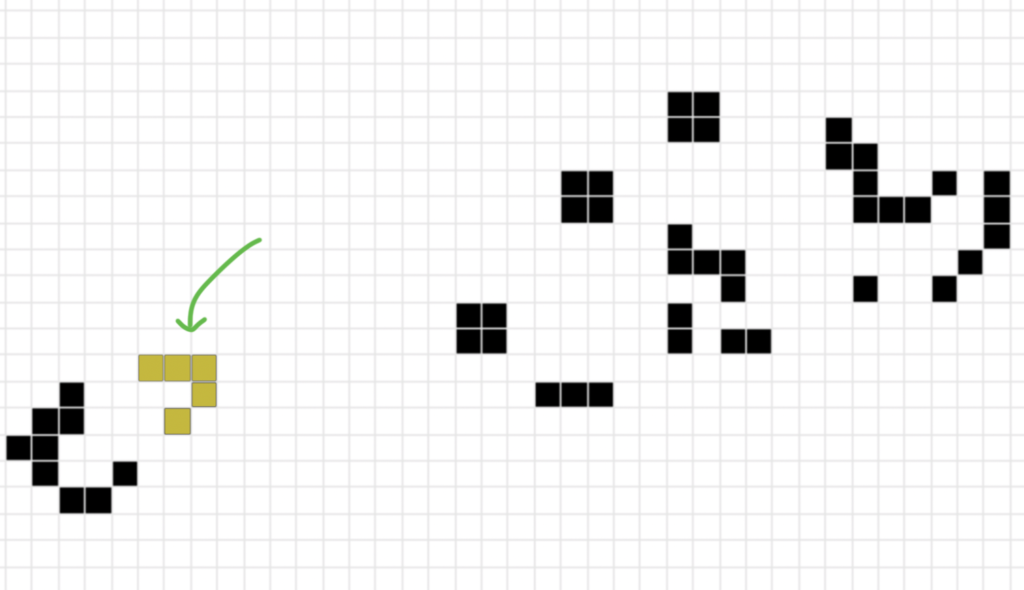
This kept moving away from the scene of chaos:

Conway was intrigued. He called this pattern the “glider”.
More about the glider in part two; get ready for more time travel!
(If you’re wondering where Von Neumann and his replication idea went, don’t worry; it’ll be addressed in a future post. I just wanted to put the idea out there.)